Ctrl+K

Information Gain (IG)

Information Gain (IG)#

Once we know how to calculate Entropy, we can measure how much uncertainty (or impurity) is reduced when we split a dataset using a feature. This reduction is called Information Gain.

Information Gain measures the reduction in entropy achieved by a split. It tells us how much uncertainty (impurity) is removed by a particular split.

Definition#

Formally, suppose a split divides the parent node \(S\) into \(V\) subsets:
$\( S_1, S_2, ..., S_V \)$

Let:

  • \(|S|\) = total number of samples in the parent node

  • \(|S_v|\) = number of samples in child node \(S_v\)

Information Gain for a feature A is defined as:

\[ IG(S, A) = Entropy(S) - \sum_{v \in Values(A)} \frac{|S_v|}{|S|} \, Entropy(S_v) \]

where:

  • \(S\) = parent node (original dataset)

  • \(A\) = feature used for splitting

  • \(S_v\) = subset of \(S\) corresponding to value \(v\) of feature \(A\)

  • \(|S|\), \(|S_v|\) = number of samples in \(S\) and \(S_v\), respectively

The algorithm selects the feature with the highest Information Gain for splitting.

Intuition#

Information Gain measures how much a split reduces impurity:

  • A high IG means the feature created purer subsets (good split).

  • A low IG means the feature did not reduce impurity much (poor split).

Decision Trees choose the feature with the highest Information Gain at each step.

Example#

Suppose a dataset has 10 samples:

  • 6 Pass, 4 Fail

Then the initial (parent) entropy is:

\[ Entropy(S) = -\left( \frac{6}{10}\log_2\frac{6}{10} + \frac{4}{10}\log_2\frac{4}{10} \right) \approx 0.971 \]

Now we split based on Feature A (e.g., “Study Hours”) which has two possible values:

  • A = High: 5 samples → 4 Pass, 1 Fail

  • A = Low: 5 samples → 2 Pass, 3 Fail

Compute entropy for each group:

\[ Entropy(S_{High}) = -\left( \frac{4}{5}\log_2\frac{4}{5} + \frac{1}{5}\log_2\frac{1}{5} \right) \approx 0.722 \]
\[ Entropy(S_{Low}) = -\left( \frac{2}{5}\log_2\frac{2}{5} + \frac{3}{5}\log_2\frac{3}{5} \right) \approx 0.971 \]

Then the weighted average entropy after splitting is:

\[ Entropy_{after} = \frac{5}{10}(0.722) + \frac{5}{10}(0.971) = 0.847 \]

Finally, the Information Gain is:

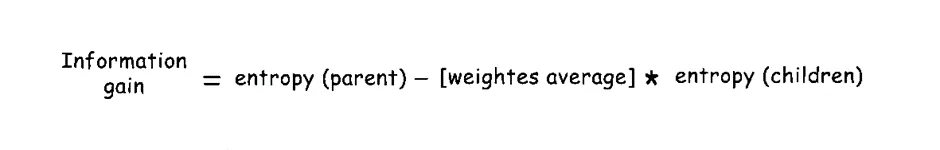
Pandas Illustration
\[ IG(S, A) = 0.971 - 0.847 = 0.124 \]

So, splitting on Feature A reduces uncertainty by 0.124 bits.

Additional Example:#

Example illustrating the calculation of information gain. Source: Hendler 2018, slide 46.

Pandas Illustration

Try it Yourself#

If you have another feature B that splits the same data into:

  • B = Yes: 6 samples (5 Pass, 1 Fail)

  • B = No: 4 samples (1 Pass, 3 Fail)

Try calculating:

\[ Entropy(S_{Yes}), \; Entropy(S_{No}), \; \text{and} \; IG(S, B) \]

Which feature gives a higher Information Gain — A or B?

import math

def entropy(class_counts):
    """
    Compute entropy for a list of class counts.
    class_counts: list of counts for each class
    """
    total = sum(class_counts)
    entropy_value = 0
    for count in class_counts:
        if count == 0:  # avoid log(0)
            continue
        p = count / total
        entropy_value -= p * math.log2(p)
    return entropy_value

def information_gain(parent_counts, split_counts_list):
    """
    Compute Information Gain.
    parent_counts: list of counts in the parent node
    split_counts_list: list of lists, each sublist contains counts in a child node
    """
    total_parent = sum(parent_counts)
    parent_entropy = entropy(parent_counts)

    weighted_entropy = 0
    for counts in split_counts_list:
        weight = sum(counts) / total_parent
        weighted_entropy += weight * entropy(counts)

    ig = parent_entropy - weighted_entropy
    return ig

# Example: Feature A split
# Parent node: 6 Pass, 4 Fail
parent = [6, 4]

# Feature A splits:
# High: 4 Pass, 1 Fail
# Low: 2 Pass, 3 Fail
split_A = [[4, 1], [2, 3]]

print("Information Gain for Feature A:", round(information_gain(parent, split_A), 3))

# Feature B splits:
# Yes: 5 Pass, 1 Fail
# No: 1 Pass, 3 Fail
split_B = [[5, 1], [1, 3]]

print("Information Gain for Feature B:", round(information_gain(parent, split_B), 3))

Information Gain for Feature A: 0.125
Information Gain for Feature B: 0.256
Contents