Ctrl+K

Central Limit Theorem (Why Normal Appears Everywhere)

Central Limit Theorem (Why Normal Appears Everywhere)#

In data science, we repeatedly see the Normal distribution, even when the original data is not normal. The reason is the Central Limit Theorem (CLT).

CLT Theorem: Regardless of the original distribution, the distribution of sample means approaches a Normal distribution as sample size increases.

Mathematically: Central Limit Theorem (Informal)

Let \(X_1, X_2, \dots, X_n\) be independent random variables with the same mean \(\mu\) and finite variance.

As \(n\) becomes large, the distribution of the sample mean

\(\bar{X} = \frac{1}{n}\sum_{i=1}^n X_i\)

approaches a Normal distribution, regardless of the original distribution of the data.

Intuition:

  • Individual data points can be messy, skewed, or discrete

  • Averages of many observations become predictable

  • Noise cancels out, and structure emerges

This is why:

  • averages of clicks

  • average model errors

  • average measurements

often behave normally, even if the raw data does not.

Central Limit Theorem Visual Overview#


Bernoulli distribution (Slideserve)
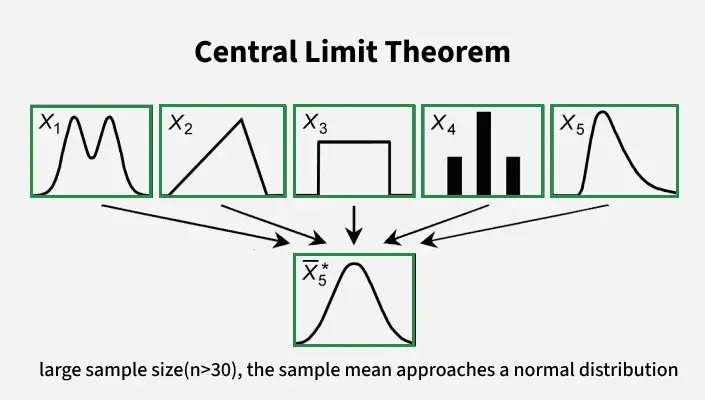Bernoulli PMF/Outcome illustration (Medium)
Bernoulli PMF/Outcome illustration (Medium)

These figures illustrate why sample means tend to follow a Normal distribution, even when the original data is not Normal.

Python Simulation: CLT in Action

We will start with data that is not normal (Uniform), then look at averages.

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

n_samples = 20_000

# Step 1: raw data (uniform, not normal)
raw = np.random.uniform(0, 1, size=n_samples)

# Step 2: averages of multiple samples
k = 30
averages = np.mean(
    np.random.uniform(0, 1, size=(n_samples, k)),
    axis=1
)

plt.figure()
plt.hist(raw, bins=40, density=True)
plt.title("Raw Data: Uniform(0,1)")
plt.xlabel("Value")
plt.ylabel("Density")
plt.show()

plt.figure()
plt.hist(averages, bins=40, density=True)
plt.title("Averages of 30 Uniform Samples (CLT)")
plt.xlabel("Value")
plt.ylabel("Density")
plt.show()
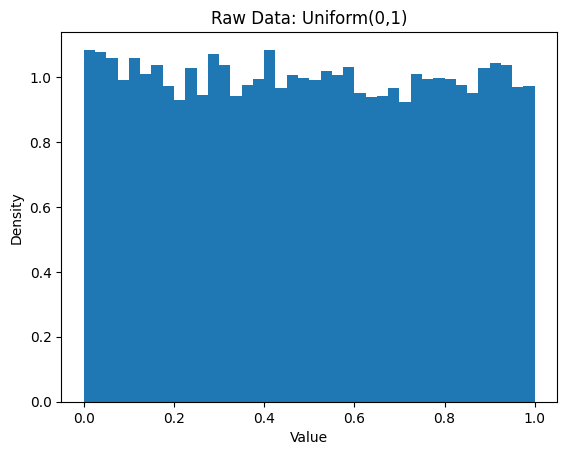
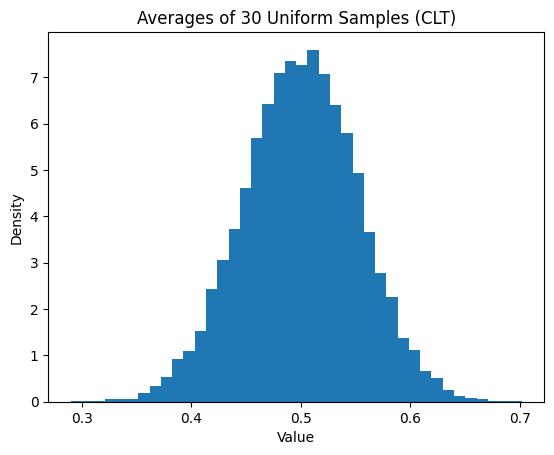
../_images/f277fb0d53b85c0236aeb07b8564dac5e1cf762e56a92977e07ce49dffd4aa52.png ../_images/f16f124b4e44b2b9917ee8039f6ad61cfa8d0a148c58e34b933e847c6108eefa.png

Notice: Even when the raw data is not bell-shaped, the averages form a bell-shaped curve. This happens without assuming normal data; this is the Central Limit Theorem at work.

Why CLT Matters in Data Science#

The Central Limit Theorem explains why we can:

  • use Normal-based confidence intervals

  • apply z-tests and t-tests

  • model average error with Gaussian assumptions

  • trust metrics based on means

Data Science Insight
Many statistical tools assume normality of averages, not raw data.
This assumption is justified by the Central Limit Theorem.

Contents