(IV) Correlation and Relationships Between Variables

So far we’ve described one variable at a time.

Now we ask:

How do two variables move together?

(IV.a) Correlation

Correlation measures the strength and direction of a linear relationship between two variables. The most common measure is Pearson’s correlation coefficient (r).

\[ -1 \leq r \leq 1 \]

Interpretation of r

r Value	Meaning
r ≈ 1	Strong positive linear relationship
r ≈ -1	Strong negative linear relationship
r ≈ 0	No linear relationship

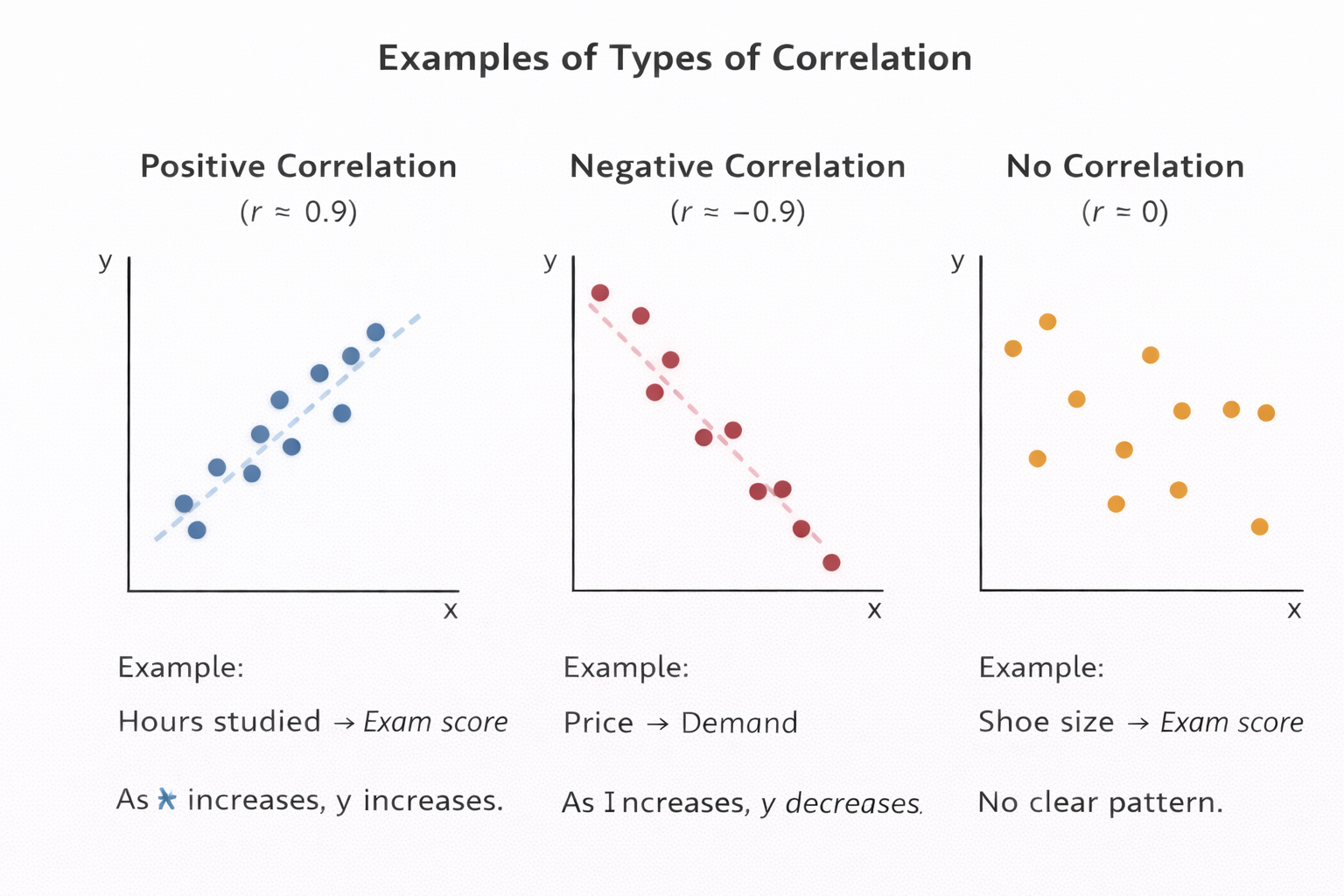
Figure: Scatter plot examples showing positive, negative, and no correlation between two variables.

• Positive: As x increases, y increases (e.g., study time and exam score)

• Negative: As x increases, y decreases (e.g., price and demand)

• None: No clear relationship (e.g., shoe size and exam score)